Skip to main content

300x250 Ads

Band Limited Signal

By Ashik

Band Limited Signal
 
A signal is said to be a band limited signal if all of its frequency components are zero above a certain finite frequency. i.e it's power spectral density should be zero above the finite frequency.
Figure 1 shows a signal g(t) that is band limited.











Bandwidth requirements (communications)
The channel bandwidths needed to transmit various types of signals, using various processing schemes. Every signal observed in practice can be expressed as a sum (discrete or over a frequency continuum) of sinusoidal components of various frequencies. The plot of the amplitude versus frequency constitutes one feature of the frequency spectrum (the other being the phase versus frequency). The difference between the highest and the lowest frequencies of the frequency components of significant amplitudes in the spectrum is called the bandwidth of the signal, expressed in the unit of frequency, hertz. Every communication medium (also called channel) is capable of transmitting a frequency band (spectrum of frequencies) with reasonable fidelity. Qualitatively speaking, the difference between the highest and the lowest frequencies of components in the band over which the channel gain remains reasonably constant (or within a specified variation) is called the channel bandwidth.
Clearly, to transmit a signal with reasonable fidelity over a communication channel, the channel bandwidth must match and be at least equal to the signal bandwidth. Proper conditioning of a signal, such as modulation or coding, however, can increase or decrease the bandwidth of the processed signal. Thus, it is possible to transmit the information of a signal over a channel of bandwidth larger or smaller than that of the original signal.
Amplitude modulation (AM) with double sidebands (DSB), for example, doubles the signal bandwidth. If the audio signal to be transmitted has a bandwidth of 5 kHz, the resulting AM signal bandwidth using DSB is 10 kHz. Amplitude modulation with a single sideband (SSB), on the other hand, requires exactly the same bandwidth as that of the original signal. In broadcast frequency modulation (FM), on the other hand, audio signal bandwidth is 15 kHz (for high fidelity), but the corresponding frequency-modulated signal bandwidth is 200 kHz.
C. E. Shannon proved that over a channel of bandwith B the rate of information transmission, C, in bits/s (binary digits per second) is given by the



equation below, where SNR is the signal-to-noise power ratio. This result assumes a white Gaussian noise, which is the worst kind of noise from the point of view of interference.
It follows from Shannon's equation that a given information transmission rate C can be achieved by various combinations of B and SNR. It is thus possible to trade B for SNR, and vice versa.
A corollary of Shannon's equation is that, if a signal is properly processed to increase its bandwidth, the processed signal becomes more immune to interference or noise over the channel. This means that an increase in transmission bandwidth (broadbanding) can suppress the noise in the received signal, resulting in a better-quality signal (increased SNR) at the receiver. Frequency modulation and pulse-code modulation are two examples of broadband schemes where the transmission bandwidth can be increased as desired to suppress noise.
Broadbanding is also used to make communication less vulnerable to jamming and illicit reception by using the so-called spread spectrum signal.








Labels:

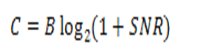
Comments

Post a Comment

Popular posts from this blog

Armature Winding ,Pole Pitch, Coil Span, Commutator Pitch

By Ashik
Now we are going to discuss about armature winding in details. Before going through this section, we should understand some basic terms related to armature winding of dc generator . Pole Pitch Definition of Pole Pitch The pole pitch is defined as peripheral distance between center of two adjacent poles in dc machine. This distance is measured in term of armature slots or armature conductor come between two adjacent pole centers. This is naturally equal to the total number of armature slots divided by number of poles in the machine. If there are 96 slots on the armature periphery and 4 numbers of poles in the machine, the numbers of armature slots come between two adjacent poles centers would be 96/4 = 24. Hence, the pole pitch of that dc machine would be 24. As it is seen that, pole pitch is equal to total numbers of armature slots divided by total numbers of poles, this can alternatively referred as armature slots per pole . Coil Span or Coil Pitch Coil of
Post a Comment
Read more

Propagation-Radio-Waves

By Ashik
Radio Wave Propagation types
Post a Comment
Read more

Coding

By Ashik
Binary Coding 1. Binary Coded Decimal (BCD) Binary coded decimal (BCD) is a way to express each of the decimal digits with a binary code. There are only ten code groups in the BCD system, so it is very easy to convert between decimal and BCD. Because welike to read and write in decimal, the BCD code provides an excellent interface to binary systems. Examples of such interfaces are keypad inputs and digital readouts. The 8421 Code: The 8421 code is a type of BCD (binary coded decimal) code. Binary coded decimal means that each decimal digit, 0 through 9, is represented by a binary code of four bits. The designation 8421indicates the binary weights of the four bits 2 3 , 2 2 , 2 1 , 2 0 . The ease  of conversion between 8421 code numbers and the familiar decimal numbers is the main advantage of this code.  All wehave to remember are the ten binary combinations that represent the ten decimal digits as shown in Table 1. The 8421 code is the predominant BCD code, and when we ref
Post a Comment
Read more

Add